Vertical Scale: How Deep the Deep Halls?
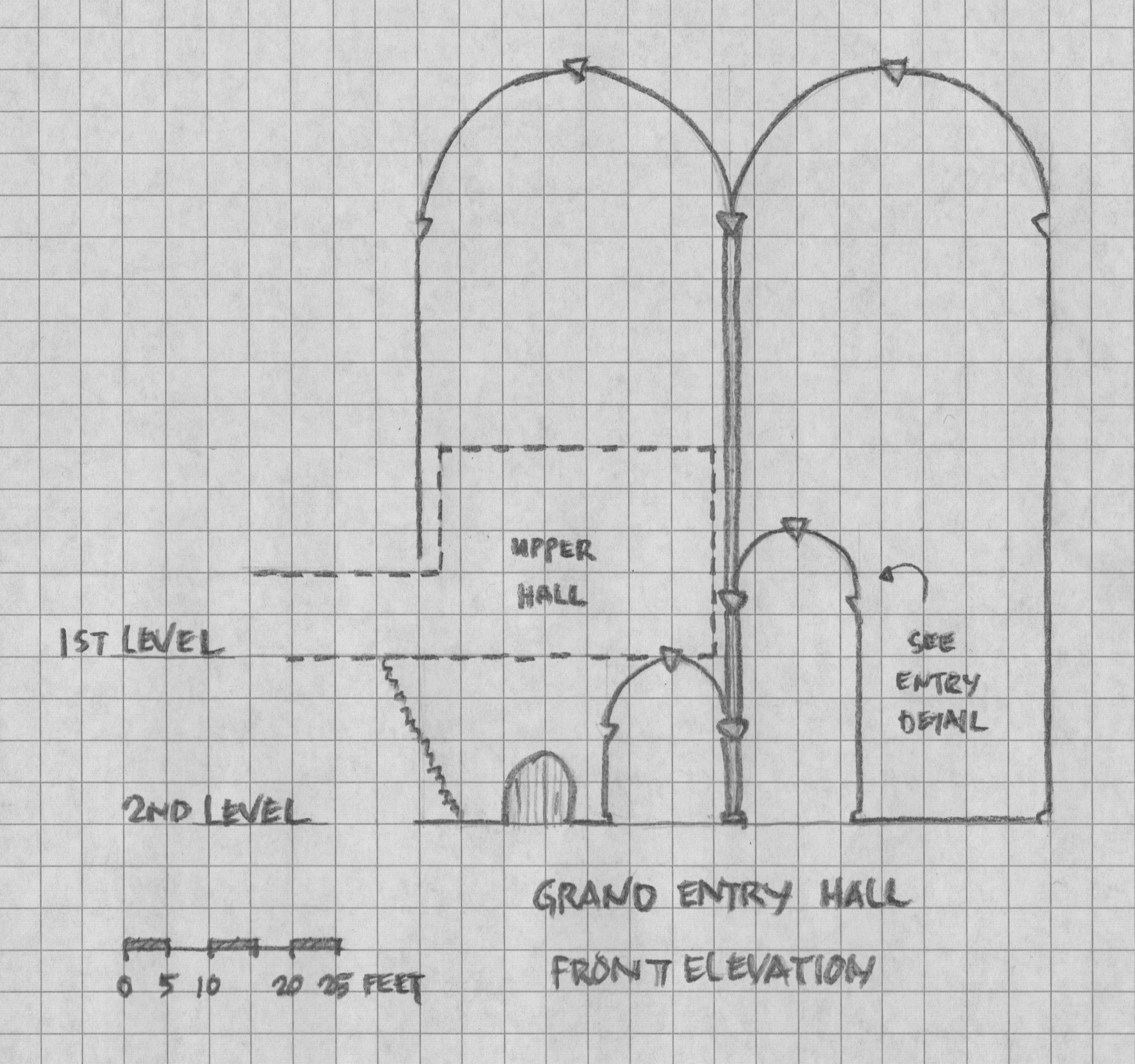
In “Channeling Amon-Gorloth,” we defined a “hall” as “any space two or more squares wide and at least twice as long.” Now, we consider the three-dimensional space, notably, ceiling heights, the incline of stairways, and how to handle intruding upper levels.
The following discussion considers only the built dungeon areas. The priests may or may not have given similar treatment to the natural caverns. We assume the horizontal scale is ten feet to the square.
How High the Ceilings?
General rules are easy to remember and give us varying heights by how we define the space as well as its width. A particular space may vary from the rules.
Definitions
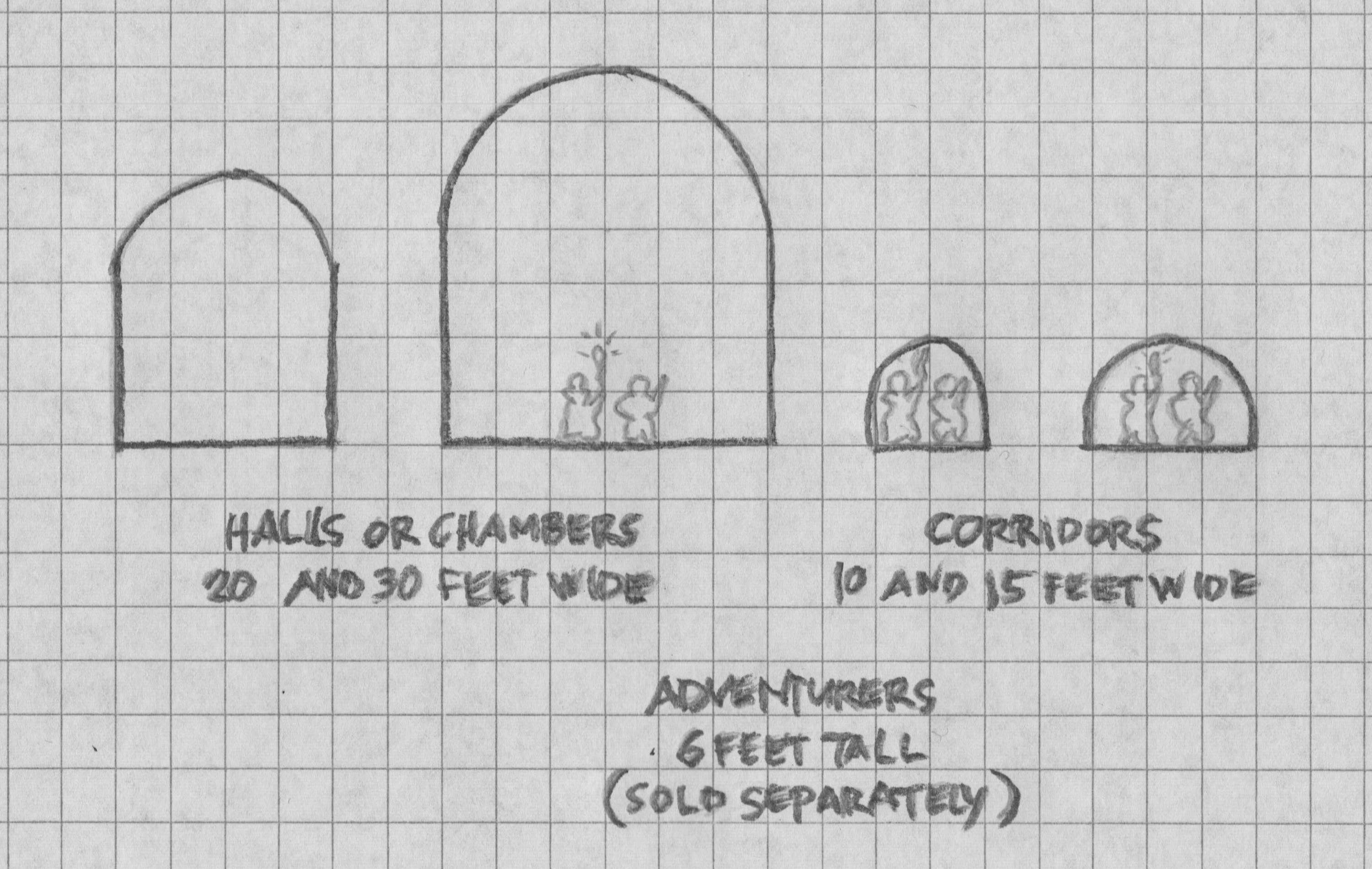
For the purpose of determining ceiling heights, we define the following spaces:
Hall: Any area at least 20 feet wide and at least twice as long as its width.
Chamber: Any area at least 20 feet wide and less than twice as long as its width.
Corridor: Any area less than 20 feet wide.
Using the entry way as an example (map above): From the outside, a corridor, part caved in, leads 30 feet into a hall. Through the door on the right, another corridor leads to a few chambers.
Halls and Chambers
As these halls are “used by the priests to some devotional purpose, including entombment” (“Channeling Amon-Gorloth”), I imagine impressive ceiling heights.
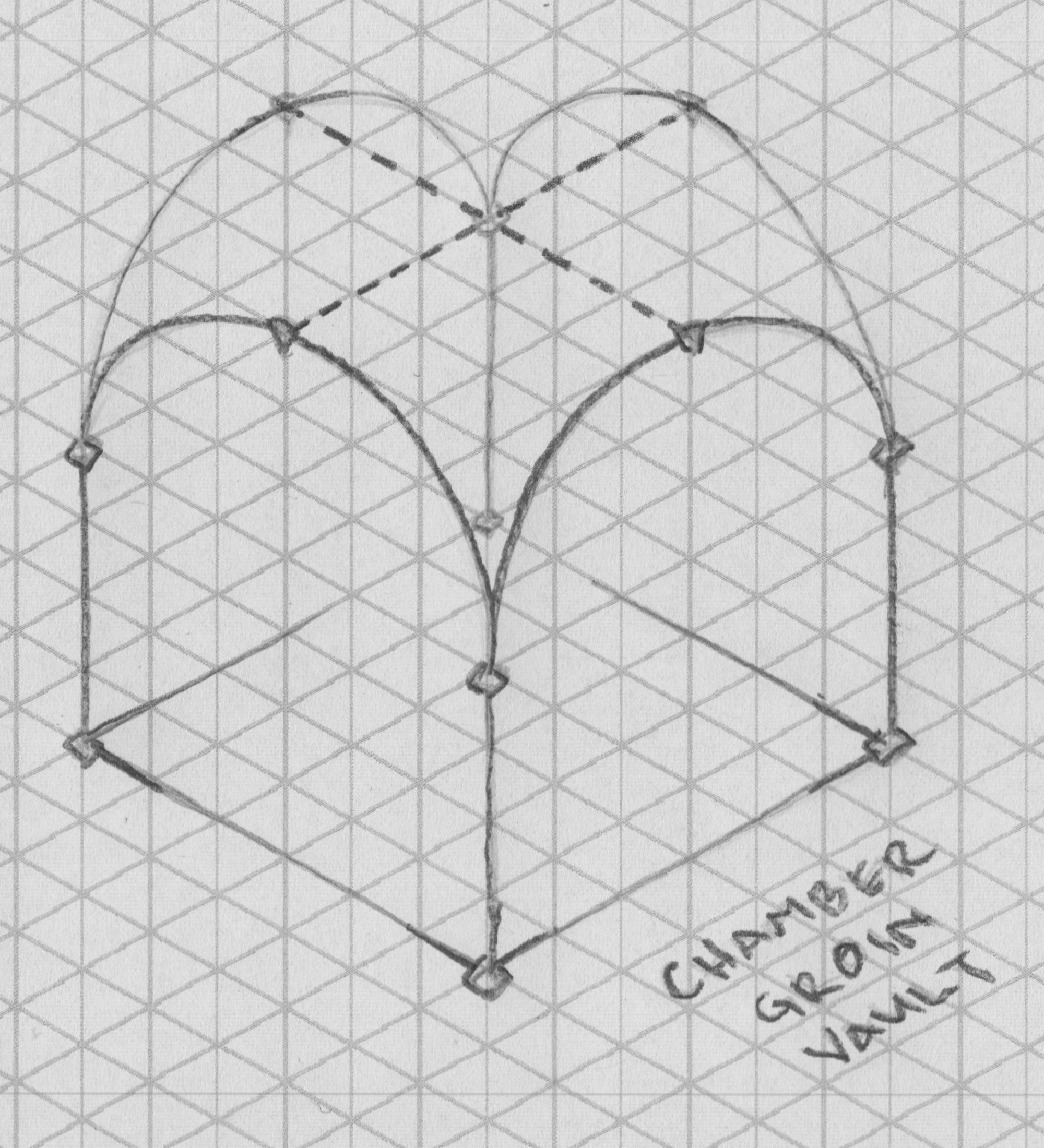
Halls and rectangular chambers are barrel vaulted, peaking at five feet higher than their width. Square chambers are groin vaulted, also five feet higher than wide.
Corridors
Corridors are barrel vaulted at only ten feet high. This makes for a cramped space—a contrast to the halls and chambers.
How Steep the Stairs?
Ever since I’ve had the imagination for such things, I assumed dungeon stairs go up and down at a 45° angle. Ten horizontal feet on the dungeon map means ten vertical feet. This makes imagining the dungeon in three dimensions simpler.
We see though, in our explorations, that these halls are not simple but “twisted and nightmarish.” The dreaming priests, in their oneiric interpretations, were forced to devise other solutions.
Typical stairs in our residential world step up at a 37° angle, rising 7.75 feet for every ten horizontal feet. According to the US Department of Labor’s Occupational Safety and Health Administration, standard stairs incline from 30° to 50° from horizontal.1 Up to 70° is considered steep. More steep is a ladder. Less than 30° is a slope.2
Angles for vertical rises of 5-30 feet over ten horizontal feet.
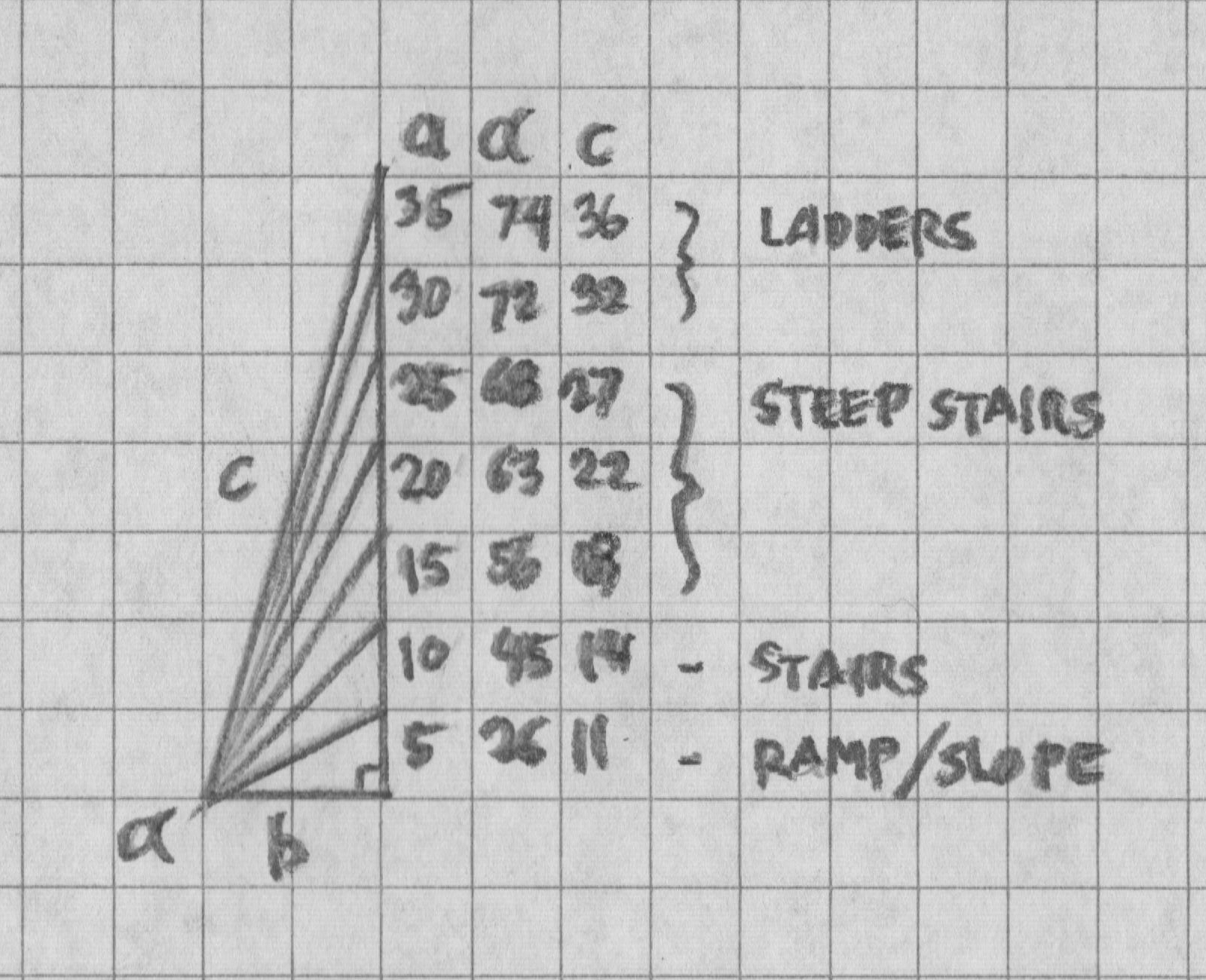
Reaching into our backpack, we pull out a slide rule or a Pythagorean theorem calculator.3 In the table below, a is a stair’s vertical rise over a ten-foot horizontal distance (b), c is the distance traveled up or down, and α is the incline from the horizontal plane.
| Table of Slopes, Stairs, and Ladders | |||
|---|---|---|---|
| a | c | α | Term |
| 35′ | 36′ | 74° | Ladder |
| 30′ | 32′ | 72° | |
| 25′ | 27′ | 68° | Steep Stairs |
| 20′ | 22′ | 63° | |
| 15′ | 18′ | 56° | |
| 10′ | 14′ | 45° | Standard Stairs |
| 5′ | 11′ | 26° | Ramp or Slope |
In our cartographic interpretations, we have considerable leeway between 30 and 70 degrees. The immediate impact of the incline is the height limitation on any space directly below another space, i.e., the distance between levels. For in the “convoluted mausoleums,” the halls and corridors of one level pass over and under those of other levels.
We find a good example in the entry hall, where we pass beneath a corner of an upper chamber.
Ten Feet, 45 Degrees: At 45 degrees, the stairs to Level 1, which occupy a ten-foot square, go up only ten feet. The lower the angle, the lower a level’s height. I would put 45 at the minimum angle. No matter the stair height, the upper level intrudes the entry. We could make it work at ten feet high, but deeper seems more appropriate in The Deep Halls.
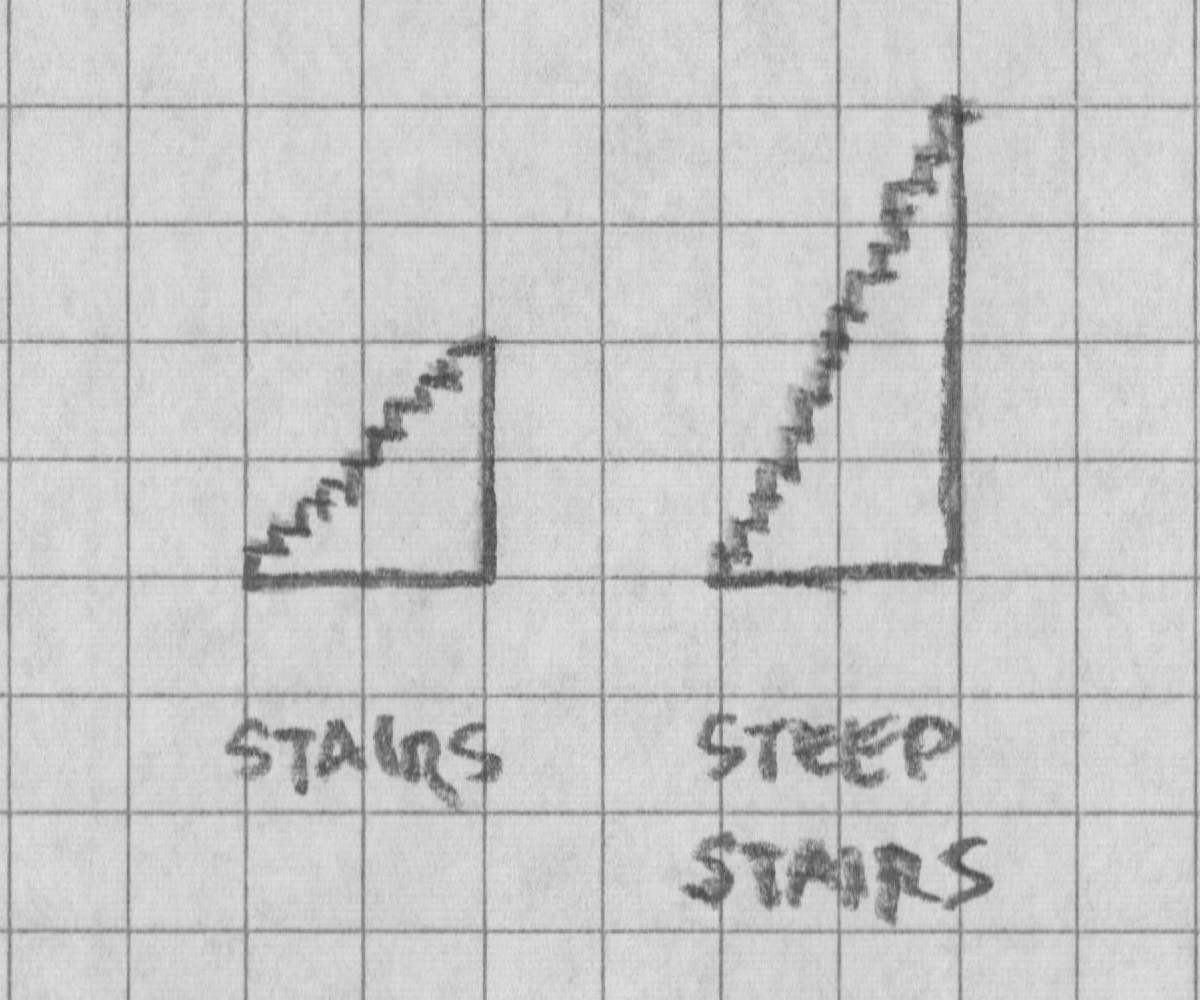
Twenty Feet, 63 Degrees: Rising 20 feet over ten horizontal, the incline is 63 degrees, approaching but not quite ladder steep. The precarious angle may well impact movement and melee (see “Optional Rules for Steep Stairs”) and might give explorers a moment of vertigo.
Upper Level Intrusions
Now that we have the ceiling height and the upper room’s position above the entryway floor, we can look at how to handle the inevitable intrusion. Here, we deal with the entryway. Other instances, encountered further on, might be handled in similar fashion.
The challenge is to respect the map. That is, we cannot add columns, walls, or other features. The best way I’ve come up with is modified groin vaulted ceilings of differing heights, side by side.
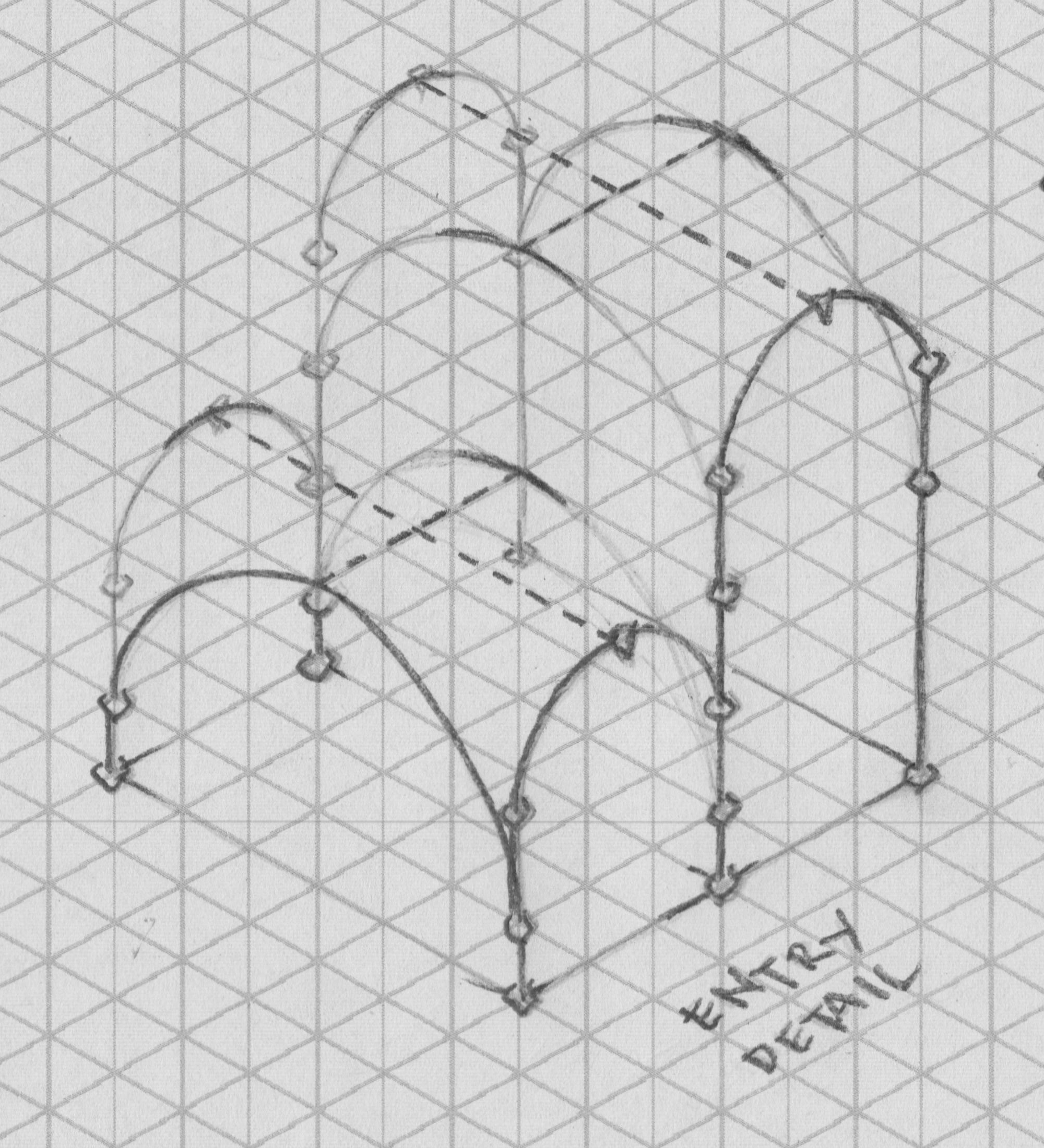
I am not certain this structure would stand. A groin vault is normally square. The cartographer’s column placement imposes a length longer than the width. To accommodate the rectangular space, I dropped the long arch’s base a few feet below that of the shorter arch.
The right vault rises to 35 feet above the floor. The left peaks at 20 feet. The upper room is supported by the vault below it.
Notes
1 1926.1052 - Stairways, Occupational Safety and Health Administration.
2 Standard Stair Angle: Typical Pitch Of A Staircase Slope By Use Case, Lapeyre Stair Blog.
3 Pythagorean Theorem Calculator, Calculator.net.